Rumus Persamaan Garis Singgung Lingkaran

materi matematika - Image from shiksha.com

Dalam kesempatan kali ini kami wajibbaca.com akan membahas tentang persamaan garis singgung lingkaran.

Disini kami akan membahas mulai dari pengertian persamaan garis singgung lingkaran hingga rumus persamaan garis singgung lingkaran.

Tanpa panjang kata, mari kita simak penjelasan dibawah ini.

Pengertian Persamaan Garis Singgung Lingkaran

Persamaan garis singgung lingkaran adalah suatu garis yang menyinggung sebuah lingkaran. Dalam bidang kartesius, lingkaran diartikan sebagai titik-titik yang jumlahnya tak hingga dan mempunyai jarak yang sama dengan pusat lingkaran.

Jarak dari tiap titik ke titik pusat disebut sebagai jari-jari r. Untuk info lengkap mengenai garis singgung lingkaran, anda simak saja ulasan yang kami bagikan di bawah ini.

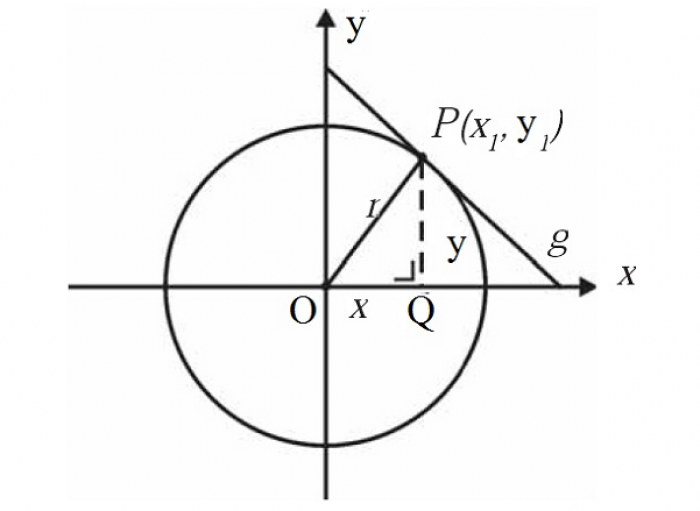
contoh garis singgung lingkaran - Image from rumusbilangan.com

Cara Menentukkan Persamaan Garis Singgung Lingkaran

Cara menentukkan persamaan garis singgung lingkaran yang akan dibahas kali ini akan dibedakan dalam 3 kondisi. 

Yang pertama adalah kondisi persamaan garis singgung yang melalui satu titik pada lingkaran. Kemudian yang kedua adalah persamaan garis singgung yang melalui satu titik di luar lingkaran. Dan yang terakhir adalah persamaan garis singgung dengan nilai gradien (m) tertentu.

Diperlukan cara yang berbeda untuk masing-masing kondisi dalam menentukan persamaan garis singgung lingkaran untuk ketiga kondisi tersebut. Selain mengetahui rumus persamaan garis singgung lingkaran. Anda juga perlu mengetahui kriteria kedudukan titik dan garis terhadap lingkaran. 

Bahkan, sebelum mempelajari cara mencari persamaan garis singgung lingkaran, Anda sudah mengetahui cara mengetahui kedudukan titik dan garis terhadap lingkaran. Kedudukan titik pada sebuah lingkaran menunjukkan posisi titik terhadap lingkaran. Kedudukan titik tersebut dapat meliputi di dalam lingkaran, pada lingkaran, dan di luar lingkaran.

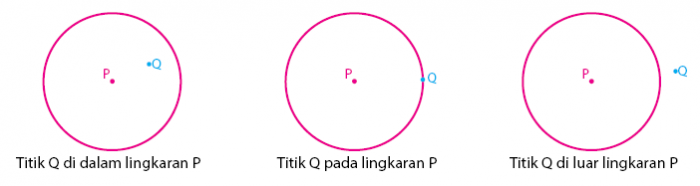
titik pada persamaan garis singgung lingkaran - Image from idschool.net

Begitu juga dengan kedudukan garis terhadap lingkaran. Meliputi pembahasan posisi garis terhadap lingkaran. Ini termasuk garis memotong lingkaran pada dua titik, garis memotong lingkaran pada satu titik (menyinggung lingkaran), atau garis terletak di luar lingkaran.

1. Garis singgung melalui suatu titik pada lingkaran

Kondisi pertama persamaan garis singgung lingkaran yang akan dibahas adalah garis singgung melalui suatu titik pada lingkaran. 

Misalkan sebuah lingkaran dengan pusat P dan diketahui titik Q yang dinyatakan dalam koordinat (x1, y1). 

Langkah berikutnya adalah mencari persamaan garis singgung yang melalui titik Q tersebut. Garis yang dimaksud adalah persamaan garis lingkaran dengan pusat P dan melalui titik Q.

Untuk contohnya bisa anda lihat pada gambar di bawah.

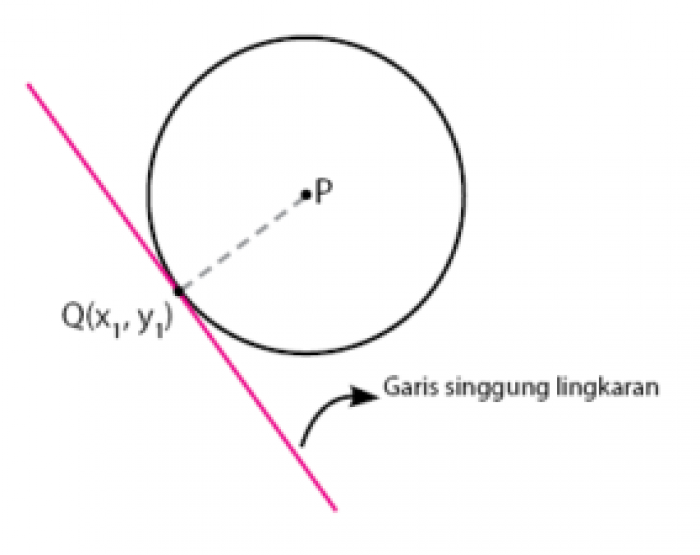
garis singgung melalui satu titik lingkaran - Image from idschool.net

Dalam garis singgung lingkaran yang melalui suatu titik pada lingkaran, ada 3 persamaan umum yang biasa digunakan.

Tentunya dengan 3 persamaan umum tersebut rumus yang akan digunakan tergantung pada bentuk persamaan lingkaran yang diketahui. 

Baca Juga: 
1. Materi Matematika Kelas 7 SMP Kurikulum 2013 Semester 1 dan 2
2. Ini Dia Beberapa Trik Matematika yang Pastinya Belum Kamu Dapet Dari Sekolah
3. Cara Mudah Mengajari Anak Matematika Dasar
4. Contoh Soal Matematika Kelas 4 Kurikulum 2013 Lengkap dengan Kunci Jawabannya

Jika titik singgung pada lingkaran adalah (x1, y1), maka rumus umum persamaan garis singgung lingkaran yang melalui suatu titik dapat dilihat pada tabel di bawah.

rumus garis singgung melalui satu titik lingkaran - Image from idschool.net

contoh soal garis singgung melalui satu titik lingkaran - Image from idschool.net

2. Garis singgung melalui suatu titik di luar lingkaran

Garis singgung yang melalui satu titik di luar lingkaran biasa disebut juga dengan garis singgung kutub atau garis singgung polar. 

Sebut saja ada sebuah titik (x1, y1) terletak di luar lingkaran, garis singgung dapat dicari dengan menarik garis lurus dari titik tersebut sehingga menyinggung lingkaran. 

Ini berarti, bisa terdapat 2 (dua) garis singgung lingkaran yang melalui titik di luar lingkaran.

Berikut contoh dari garis singgung suatu titik di luar lingkaran.

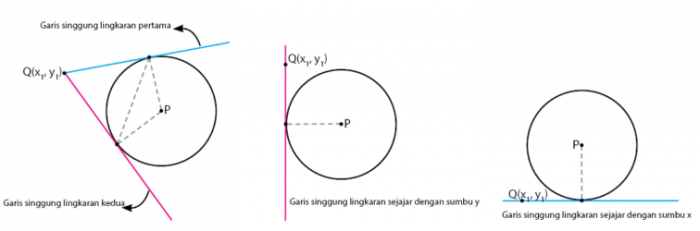
contoh garis singgung suatu titik diluar lingkaran - Image from idschool.net

Langkah-langkah dalam menentukan garis singgung suatu titik diluar lingkaran :

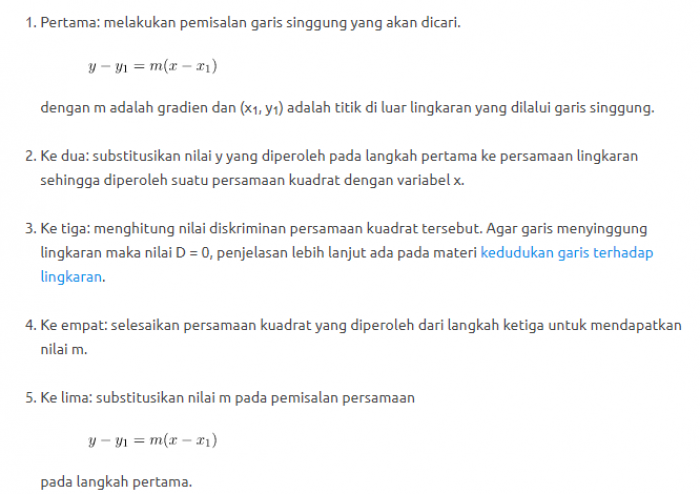
langkah-langkah garis singgung suatu titik luar lingkaran - Image from idschool.net

3. Garis singgung lingkaran dengan gradien tertentu

Ada 3 (tiga) persamaan umum yang dapat digunakan untuk menentukan garis singgung lingkaran yang diketahui nilai gradiennya. 

Seperti halnya garis singgung suatu titik pada lingkaran, rumus yang akan digunakan tergantung pada persamaan lingkaran yang diketahui.

Ketika diketahui gradien dari suatu gradien garis singgung adalah m, maka rumus umum persamaan garis singgung lingkaran untuk tiga bentuk persamaan lingkaran yang berbeda dapat dilihat pada tabel di bawah.

rumus garis singgung 4 - Image from idschool.net

contoh soal garis singgung gradien - Image from idschool.net

Demikian dari kami pembahasan tentang persamaan garis singgung lingkaran. Semoga artikel ini dapat membantu anda dalam memahami materi tersebut.