
trigonometri - Image from thegreatcoursesplus.com
Trigonometri adalah sebuah cabang matematika yang berhadapan dengan sudut segitiga dan fungsi trigonometrik seperti sinus, cosinus dan tangen. Kata Trigonometri sendiri diambil dari bahasa Yunani yaitu (Trigonon = tiga sudut) dan (metro = mengukur).
Ada pendapat bahwa trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya bagi beberapa orang, trigonometri adalah bagian dari geometri.
Berikut kami beri penjelasan tentang trigonometri dan berbagai contoh soal.
Baca Juga : Cara Cepat Mencari Rumus Deret Geometri + Contoh Soal Lengkap
Sejarah Singkat
Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu.
Matematikawan dari India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri.
Konsep Perbandingan Trigonometri
Dasar dari Trigonometri adalah Konsep kesebangunan segitiga siku-siku. Perbandingan yang sama pada sisi-sisi yang bersesuaian pada dua bangun datar yang sebangun.
Pada geometri Euclid, dua segitiga dikatakan sebangun apabila masing-masing sudut pada kedua segitiga tersebut memiliki besar yang sama.
Penjelasan di atas adalah dasar untuk perbandingan trigonometri sudut lancip. Konsep pengertian ini lalu dikembangkan lebih lanjut untuk sudut-sudut non lancip (lebih dari 90 derajat dan kurang dari nol derajat).
Menarik dibaca : Pusing Mikir Terus? Begini Cara Menghafal Rumus Matematika Dengan Mudah dan Cepat
Trigonometri Dalam Kehidupan Sehari-hari
- Sebagai teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat.
- Dapat digunakan di bidang geografi untuk menghitung antara titik tertentu dan dalam sistem navigasi satelit.
- Dalam kriminologi, trigonometri dapat membantu menghitung lintasan proyektil, untuk memperkirakan apa yang mungkin menyebabkan tabrakan dalam kecelakaan mobil atau bagaimana benda jatuh dari suatu tempat atau di mana sudut tembakan peluru, dll.
- Dalam konstruksi kita membutuhkan trigonometri untuk menghitung? Mengukur bidang, banyak dan area? Membuat dinding sejajar dan tegak lurus? memasang ubin keramik, kecenderungan atap, tinggi bangunan, panjang lebar dan sebagainya. Banyak hal lain lainnya yang menjadi kebutuhan untuk menggunakan trigonometri.
- Arsitek menggunakan trigonometri untuk menghitung beban struktural, lereng atap, permukaan tanah dan banyak aspek lainnya, termasuk sudut cahaya dan naungan matahari.
- Contoh bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanik, teknik sipil, grafik komputer, kartografi, kristalografi.
Hubungan Fungsi dan Rumus Trigonometri
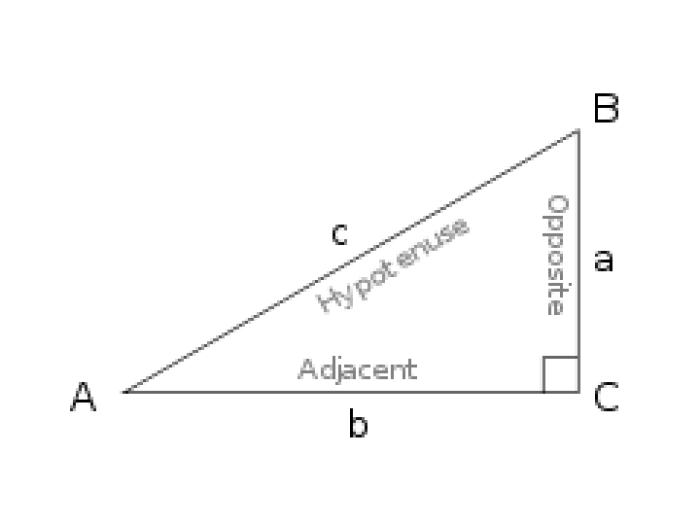
sudut segitiga pada trigonometri - Image from pinterpandai.com
Fungsi dasar Trigonometri
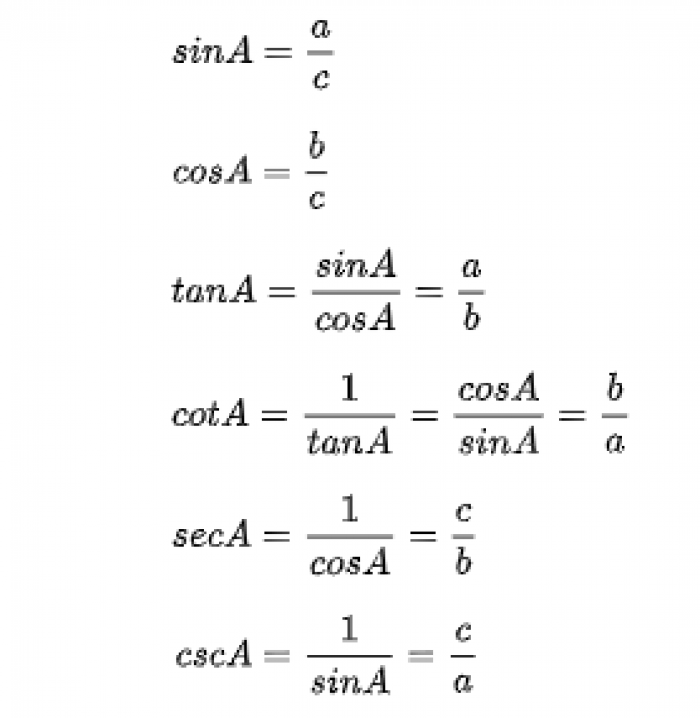
fungsi dasar - Image from pinterpandai.com
Identitas Trigonometri
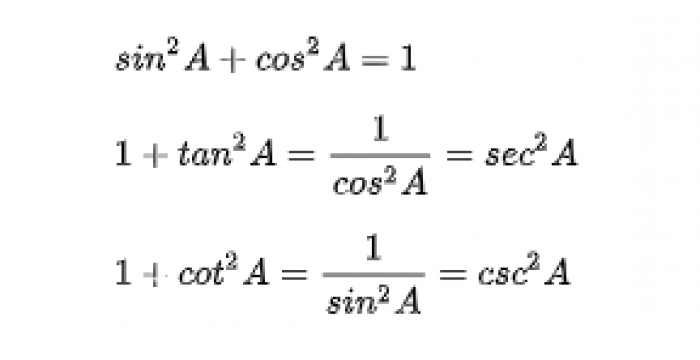
identitas trigonometri - Image from pinterpandai.com
Rumus dan Selisih Sudut

rumus jumlah dan selisih sudut - Image from pinterpandai.com
Rumus Perkalian Trigonometri
Rumus Jumlah dan Selisih Trigonometri
Rumus Sudut Rangkap Dua
Rumus Sudut Rangkap Tiga
Rumus Setengah Sudut
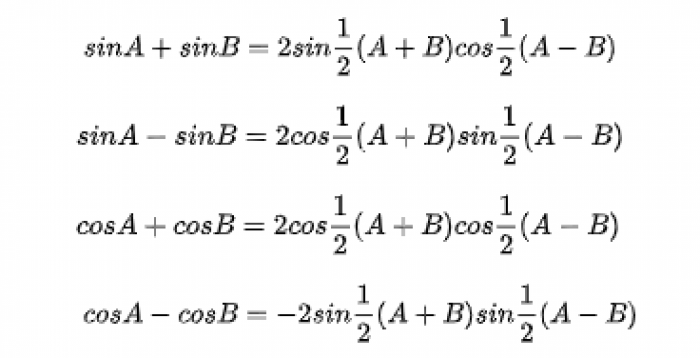
rumus jumlah dan selisih trigonometri - Image from pinterpandai.com
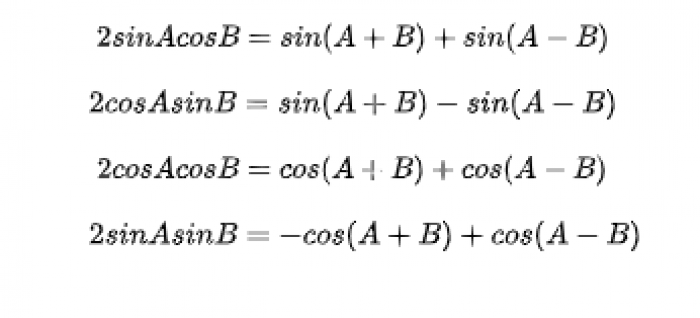
rumus perkalian trigonometri - Image from pinterpandai.com
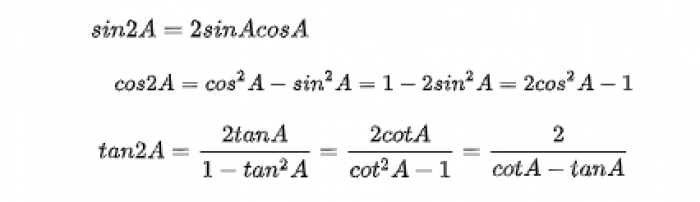
rumus sudut rangkap dua - Image from pinterpandai.com
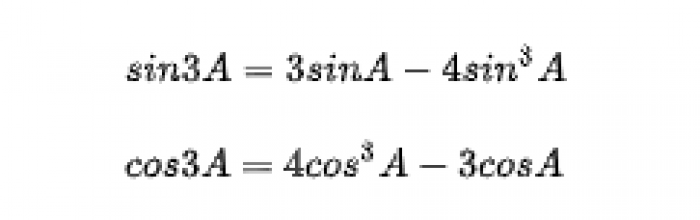
rumus sudut rangkap tiga - Image from pinterpandai.com
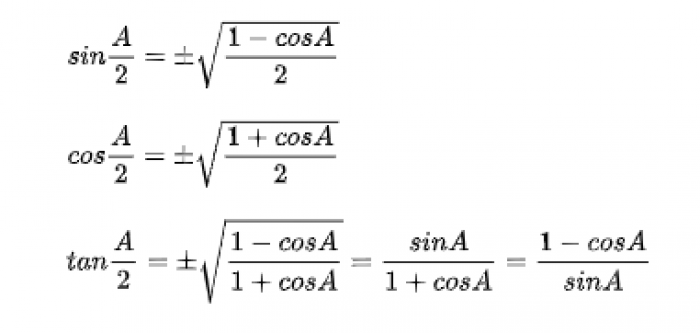
rumus setengah sudut - Image from pinterpandai.com
Perbandingan Trigonometri di Setiap Kuadran
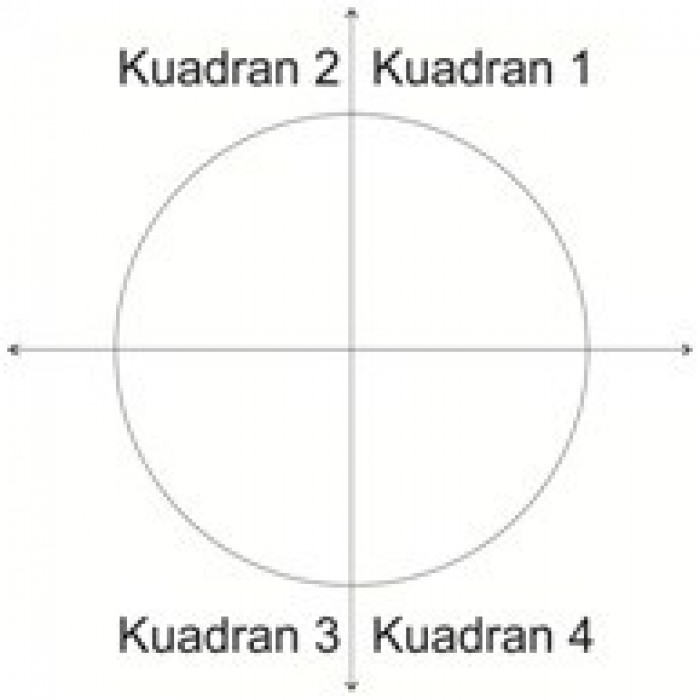
kuadran trigonometri - Image from pinterpandai.com
- Kuadran 1 memiliki rentang sudut dari 0° – 90° dengan nilai sinus, cosinus dan tangent positif.
- Kuadran 2 memiliki rentang sudut dari 90° – 180° dengan nilai cosinus dan tangen negatif, sinus positif.
- Kuadran 3 memiliki rentang sudut dari 180° – 270° dengan nilai sinus dan cosinus negatif, tangen positif.
- Kuadran 4 memiliki rentang sudut dari 270° – 360° dengan nilai sinus dan tangent negatif, cosinus positif.
Perbandingan Trigonometri Sudut Istimewa
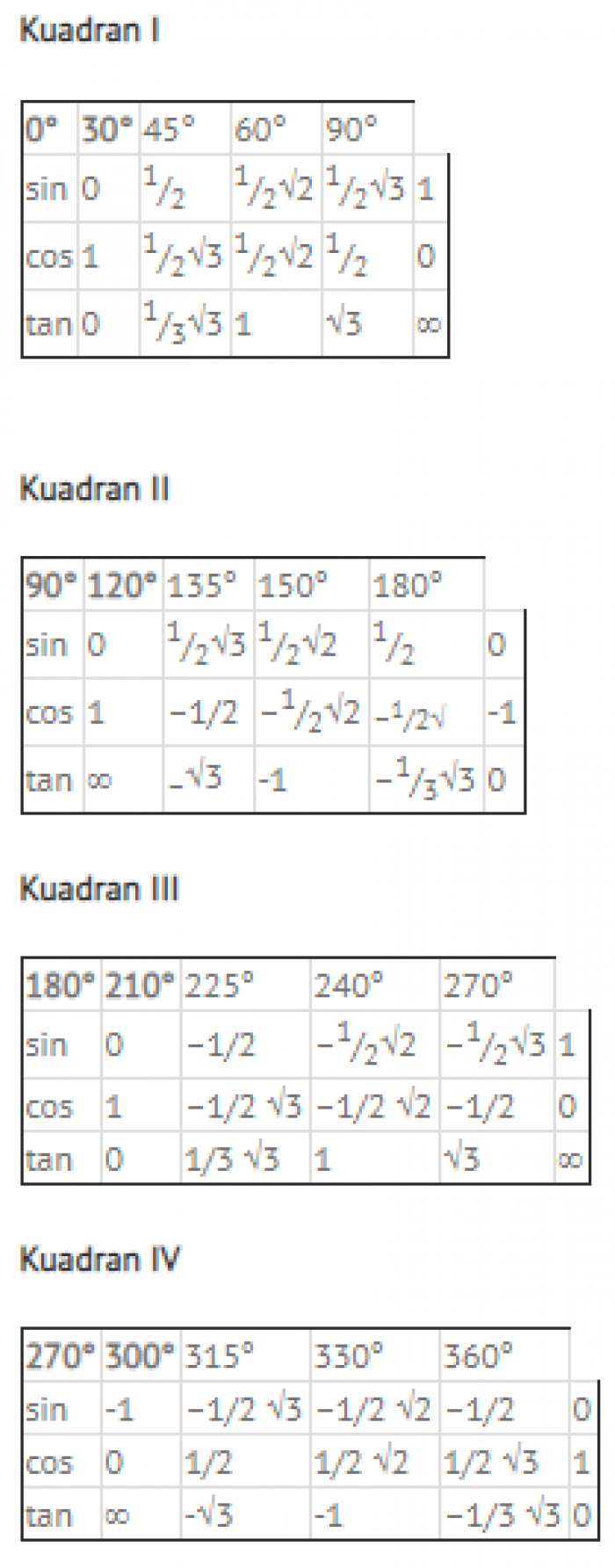
kuadran trigonometri - Image from pinterpandai.com
Contoh Soal Perbandingan Trigonometri
1. Tentukanlah nilai dari sin 120°+cos 201°+cos 315°!
Jawab:
sin 120° berada pada kuadran 2, hingga nilainya tetap positif dengan besar sama seperti sin 120° = sin (180-60)° = sin 60° = 1/2 √3
cos 120° berada pada kuadran 3, hingga nilainya negatif dengan besar sama seperti cos 120° = cos (180+30)° = – cos 30° = -1/2 √3
cos 315° berada pada kuadran 4, hingga nilainya positif dengan besar sama seperti cos 315° = cos (360-45)° = cos 45° = 1/2 √2
2. Diketahui siku-siku ABC, siku-siku di C, panjang a = 4 dan b = 3.
Tentukanlah panjang sisi dan nilai perbandingan trigonometri sudut α
Jawab:

contoh soal 2 - Image from rumus.co.id
Demikianlah penjelasan dari kami tentang perbandingan trigonometri. Jika masih ada yang belum jelas silahkan gunakan kolom komentar.
Baca Juga : Sifat Sifat Logaritma