Rumus Barisan dan Deret Aritmatika

baris dan deret - Image from jagranjosh.com

Kembali lagi di wajibbaca.com yang pada kesempatan kali ini kami akan membahas materi matematika. Materi matematika yang akan kami bahas kali ini adalah barisan dan deret aritmatika.

Materi ini sebenarnya sudah diajarkan sejak siswa menginjak bangku SMP. Namun bagi anda yang merasa ingin mempelajari lagi atau masih kurang paham, disini kami akan mencoba memberikan materi barisan dan deret aritmatika beserta contohnya.

Pengertian Barisan dan Deret Aritmatika

Pernahkan anda menghitung jumlah uang saku anda ketika sekolah, kira – kira setiap tahunnya jumlah uang saku anda berbeda – beda. Semisal uang saku anda waktu kelas satu SD adalah 2000, kemudian waktu kelas 2 SD adalah 4000, dan begitu seterusnya sampai anda lulus.

Maka jumlah uang saku yang berbeda – beda tersebut bisa dibilang telah menggambarkan dari materi yang akan kita bahas pada bab ini, yaitu barisan aritmatika.

1. Pengertian Baris Aritmatika

A. Pengertian barisan

Barisan adalah sebuah urutan dari suatu anggota-anggota himpunan yang berdasarkan suatu aturan tertentu. Pada setiap anggota himpunan diurutkan pada urutan/suku pertama, kedua, dan seterusnya.

Untuk menyatakan sebuah urutan / suku ke-n dari suatu barisan dapat dinotasikan dengan lambang U_n .

Barisan juga bisa didefinisikan sebagai fungsi dari bilangan asli atau fungsi yang domainnya adalah merupakan himpunan bilangan asli. Sehingga, U_n = f(n).

contoh barisan - Image from rumusbilangan.com

B. Pengertian baris aritmatika

Baris aritmatika adalah sebuah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui penjumlahan atau pengurangan dengan suatu bilangan b. Selisih antara nilai suku-suku yang berdekatan tersebut selalu sama yaitu b.

Maka :

U_n - U_{(n - 1)} = b

Contohnya adalah baris 1, 3, 5, 7, 9, adalah baris aritmatika dengan nilai:

b = (9 – 7) = (7 – 5) = (5 – 3) = (3 – 1) = 2

Untuk mengetahui nilai suku ke-n dari suatu barisan aritmatika, dapat kita ketahui dengan mengetahui nilai suku ke-k dan selisih antar suku yang berdekatan (b).

Rumusannya berikut ini:

U_n = U_k + (n - k)b
Apabila yang diketahui merupakan nilai suku pertama U_k = a dan selisih antar sukunya (b), maka nilai k = 1 dan nilai U_n ialah:

U_n = a + (n - 1)b

2. Pengertian Deret Aritmatika

Deret aritmatika merupakan penjumlahan antar suku-suku dari suatu barisan aritmatika. Penjumlahan dari suku-suku pertama sampai suku ke-n barisan aritmatika tersebut dapat dihitung sebagai:

Baca Dulu : Tips Mudah Belajar Matematika

S_n = U_1 + U_2 + U_3 + \cdots + U_{(n-1)}
atau sebagai =

S_n + a + (a + b) + (a + 2b) + \cdots + (a + (n - 2)b) + (a + (n - 1)b)

Jika hanya diketahui nilai a adalah suku pertama dan nilainya merupakan suku ke-n, maka nilai deret aritmatikanya yaitu:

S_n = \frac{n}{2}(a + U_n)
Persamaan tersebut dapat dibalik untuk mencari nilai suku ke-n menjadi:

S_n = U_1 + U_2 + U_3 + \cdots +U_(n-1).

S_(n-1) = U_1 + U_2 + U_3 + \cdots + U_(n-1).

S_n - S_(n-1) = U_n
Sehingga diperoleh sebagai berikut: U_n = S_n - S_(n-1).

Rumus Barisan dan Deret Aritmatika

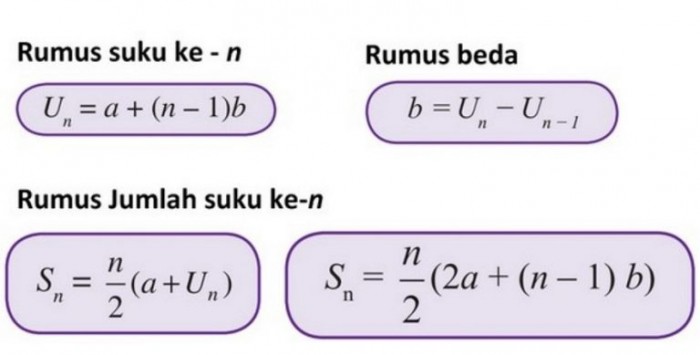
rumus barisan dan deret - Image from rumus.co.id

Barisan dari aritmatika dapat diartikan yang artinya adalah susunan bilangan yang real dan membentuk pola tertentu. 

Kemudian arti dari deret aritmatika sendiri adalah sebuah penjumlahan dari barisan aritmatika. 

Dan ciri – ciri umum nya dari barisan aritmatika yaitu mempunyai beda yang sama dari satu bilangan ke bilangan yang berikut nya. Contoh dari barisan aritmatika adalah seperti di bawah ini :

Contoh dari barisan di atas mempunyai nilai beda yaitu 8 ( b = 8 ). Berikutnya kami akan bahas lebih dalam lagi soal rumus, barisan, dan deret dari aritmatika.

1. Barisan Aritmatika

Baris aritmatika => a a + b a + 2b … a + ( n – 1 ) b

Beda => +b +b

Pengertian dari barisan aritmatika sendiri adalah sebuah barisan dengan selisih antara 2 suku yang berurutan selalu tetap. 

Dan selisih antara 2 suku yang berurutan pada barisan aritmatika ini disebut dengan beda ( b ). Berikut contoh rumus untuk menentukan beda pada suatu barisan di aritmatika.

b = Un – Un-1
 
selisihnya adalah ( b ), suku ke – n nya adalah ( Un dan Un-1 )

Kemudian di bawah ini adalah rumus suku ke – n suatu barisan di aritmatika.

Rumus Ke – n

Un = a + ( n – 1 ) b

Keterangan :

• a = suku pertama​
• b = beda
• Un = suku ke – n
• n = bilangan bulat

Ternyata ada juga rumus yang bisa kita gunakan untuk menentukan suku tengah nya dari sebuah barisan aritmatika. Dan rumus ini di gambar kan seperti contoh di bawah ini :

Rumus Aritmatika Suku Tengah

Ut = 1/2 ( U1 + Un )

Keterangan :

• a ( U1 ) = suku pertama
• Ut = suku tengah
• Un = suku ke – n
• n = bilangan bulat

2. Deret Aritmatika

Barisan aritmatika menyatakan bahwa susunan bilangan nya berurutan u1 , u2 , … , un dengan urutan tertentu. 

Sedangkan pada deret aritmatika, untuk pembahasannya adalah mengenai jumlah suku – suku berurutan tersebut. 

Untuk contoh bentuk umum dari deret aritmetika adalah seperti di bawah ini.

U1 + U2 + U3 + … + Un
 
Dengan u1 , u2 , … , un merupakan barisan dari aritmetika.

Untuk rumus nya bisa kalian lihat di bawah ini :

Rumus Penting Deret Aritmatika

• Un = Sn – Sn – 1​
• Sn = n/2 ( a + Un )
• Sn = n/2 ( 2a + ( n – 1 ) b )

Contoh Soal Aritmatika

Suatu deret aritmatika mempunyai suku ke-5 sama dengan 42, dan suku ke-8 sama dengan 15. Jumlah 12 suku pertama deret tersebut adalah?

Baca Juga: Pusing Mikir Terus? Begini Cara Menghafal Rumus Matematika Dengan Mudah dan Cepat

Pembahasan:

Diketahui bahwa U_5 = 42, U_8 = 15, maka dapat digunakan sebuah rumus sebagai berikut:
U_n = U_k + (n - k)b
Yang mana:
U_8 = U_5 + (8 - 5)b
15 = 42 + (8 - 5)b
3b = -27
b = -9
Sehingga hasilnya:
U_5 = 42 = a + 4b = a + 4(-9) = a - 36
78 = a
U_{12} = a + 11b = 78 + 11(-9) = 78 - 99 = -21
Sehingga dapat di peroleh:
S_{12} = \frac{n}{2} (a + U_12) = \frac{12}{2} (78 + (-21)) = 6 \times 57 = 342

Sekian dari kami tentang pembahasan barisan dan deret aritmatika. Semoga dengan artikel ini dapat membantu anda lebih memahami tentang konsep barisan dan deret aritmatika.